what is the angle of the wall of a tetrahedron to the ground

Polyhedron with 4 faces

Regular tetrahedron
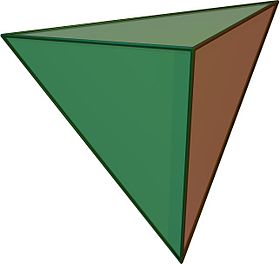(Click here for rotating model)
Type	Platonic solid
shortcode	3> 2z
Elements	F = 4, E = 6 5 = 4 (χ = two)
Faces by sides	four{3}
Conway notation	T
Schläfli symbols	{iii,iii}
	h{4,3}, s{ii,iv}, sr{2,ii}
Face configuration	V3.3.3
Wythoff symbol	3 | two iii | 2 2 ii
Coxeter diagram	=
Symmetry	Td, Aiii, [iii,three], (*332)
Rotation group	T, [3,3]+, (332)
References	U01, C15, W1
Backdrop	regular, convexdeltahedron
Dihedral angle	70.528779° = arccos( 1⁄3 )
iii.3.3 (Vertex effigy)	Cocky-dual (dual polyhedron)
Internet

3D model of regular tetrahedron.

In geometry, a tetrahedron (plural: tetrahedra or tetrahedrons), likewise known as a triangular pyramid, is a polyhedron composed of 4 triangular faces, six straight edges, and four vertex corners. The tetrahedron is the simplest of all the ordinary convex polyhedra and the just 1 that has fewer than 5 faces.^[1]

The tetrahedron is the three-dimensional case of the more general concept of a Euclidean simplex, and may thus also be called a three-simplex.

The tetrahedron is one kind of pyramid, which is a polyhedron with a flat polygon base and triangular faces connecting the base to a mutual point. In the case of a tetrahedron the base is a triangle (any of the four faces can be considered the base), so a tetrahedron is also known every bit a "triangular pyramid".

Similar all convex polyhedra, a tetrahedron tin exist folded from a single canvass of paper. It has two such nets.^[1]

For any tetrahedron there exists a sphere (chosen the circumsphere) on which all iv vertices lie, and another sphere (the insphere) tangent to the tetrahedron's faces.^[ii]

Regular tetrahedron [edit]

A regular tetrahedron is a tetrahedron in which all four faces are equilateral triangles. It is ane of the five regular Platonic solids, which have been known since antiquity.

In a regular tetrahedron, all faces are the same size and shape (congruent) and all edges are the aforementioned length.

5 tetrahedra are laid apartment on a plane, with the highest three-dimensional points marked as i, two, 3, 4, and 5. These points are then attached to each other and a thin volume of empty infinite is left, where the five edge angles do non quite meet.

Regular tetrahedra alone practice not tessellate (fill space), but if alternated with regular octahedra in the ratio of two tetrahedra to one octahedron, they course the alternated cubic honeycomb, which is a tessellation. Some tetrahedra that are non regular, including the Schläfli orthoscheme and the Loma tetrahedron, can tessellate.

The regular tetrahedron is self-dual, which means that its dual is another regular tetrahedron. The chemical compound effigy comprising two such dual tetrahedra form a stellated octahedron or stella octangula.

Coordinates for a regular tetrahedron [edit]

The following Cartesian coordinates define the four vertices of a tetrahedron with edge length 2, centered at the origin, and two level edges:

${\displaystyle \left(\pm ane,0,-{\frac {1}{\sqrt {2}}}\right)\quad {\mbox{and}}\quad \left(0,\pm one,{\frac {1}{\sqrt {2}}}\right)}$

Expressed symmetrically every bit 4 points on the unit of measurement sphere, centroid at the origin, with lower face level, the vertices are:

${\displaystyle v_{1}=\left({\sqrt {\frac {8}{ix}}},0,-{\frac {ane}{3}}\right)}$

${\displaystyle v_{2}=\left(-{\sqrt {\frac {2}{9}}},{\sqrt {\frac {ii}{3}}},-{\frac {1}{3}}\right)}$

${\displaystyle v_{iii}=\left(-{\sqrt {\frac {two}{9}}},-{\sqrt {\frac {ii}{3}}},-{\frac {ane}{3}}\correct)}$

${\displaystyle v_{four}=(0,0,1)}$

with the edge length of ${\displaystyle {\sqrt {\frac {8}{3}}}}$ .

Still some other set of coordinates are based on an alternated cube or demicube with edge length 2. This form has Coxeter diagram and Schläfli symbol h{4,3}. The tetrahedron in this case has edge length 2√ii . Inverting these coordinates generates the dual tetrahedron, and the pair together grade the stellated octahedron, whose vertices are those of the original cube.

Tetrahedron: (ane,ane,1), (1,−1,−i), (−1,1,−1), (−1,−1,i)

Dual tetrahedron: (−1,−1,−1), (−1,1,one), (1,−1,1), (1,1,−1)

Regular tetrahedron ABCD and its confining sphere

Angles and distances [edit]

For a regular tetrahedron of edge length a:

Confront area	${\displaystyle A_{0}={\frac {\sqrt {3}}{4}}a^{2}\,}$
Surface area[3]	${\displaystyle A=four\,A_{0}={\sqrt {three}}a^{ii}\,}$
Height of pyramid[iv]	${\displaystyle h={\frac {\sqrt {half dozen}}{3}}a={\sqrt {\frac {2}{three}}}\,a\,}$
Centroid to vertex altitude	${\displaystyle {\frac {iii}{4}}\,h={\frac {\sqrt {half-dozen}}{4}}\,a={\sqrt {\frac {iii}{8}}}\,a\,}$
Edge to contrary edge distance	${\displaystyle l={\frac {i}{\sqrt {ii}}}\,a\,}$
Volume[3]	${\displaystyle V={\frac {i}{iii}}A_{0}h={\frac {\sqrt {ii}}{12}}a^{3}={\frac {a^{3}}{6{\sqrt {2}}}}\,}$
Face-vertex-edge angle	${\displaystyle \arccos \left({\frac {1}{\sqrt {3}}}\correct)=\arctan \left({\sqrt {2}}\right)\,}$ (approx. 54.7356°)
Confront-edge-face angle, i.e., "dihedral angle"[three]	${\displaystyle \arccos \left({\frac {ane}{3}}\right)=\arctan \left(2{\sqrt {ii}}\right)\,}$ (approx. 70.5288°)
Vertex-Middle-Vertex angle,[five] the angle between lines from the tetrahedron center to any two vertices. Information technology is besides the angle betwixt Plateau borders at a vertex. In chemistry it is chosen the tetrahedral bond angle. This bending (in radians) is also the arclength of the geodesic segment on the unit of measurement sphere resulting from centrally projecting one edge of the tetrahedron to the sphere.	${\displaystyle \arccos \left(-{\frac {i}{3}}\right)=2\arctan \left({\sqrt {2}}\right)\,}$ (approx. 109.4712°)
Solid bending at a vertex subtended by a face	${\displaystyle \arccos \left({\frac {23}{27}}\correct)}$ (approx. 0.55129 steradians) (approx. 1809.viii foursquare degrees)
Radius of circumsphere[3]	${\displaystyle R={\frac {\sqrt {6}}{4}}a={\sqrt {\frac {3}{eight}}}\,a\,}$
Radius of insphere that is tangent to faces[three]	${\displaystyle r={\frac {i}{3}}R={\frac {a}{\sqrt {24}}}\,}$
Radius of midsphere that is tangent to edges[3]	${\displaystyle r_{\mathrm {M} }={\sqrt {rR}}={\frac {a}{\sqrt {8}}}\,}$
Radius of exspheres	${\displaystyle r_{\mathrm {Due east} }={\frac {a}{\sqrt {six}}}\,}$
Distance to exsphere heart from the opposite vertex	${\displaystyle d_{\mathrm {VE} }={\frac {\sqrt {6}}{ii}}a={\sqrt {\frac {3}{2}}}a\,}$

With respect to the base of operations plane the slope of a confront (ii√ii ) is twice that of an edge (√2 ), corresponding to the fact that the horizontal altitude covered from the base of operations to the apex forth an edge is twice that along the median of a face. In other words, if C is the centroid of the base, the distance from C to a vertex of the base is twice that from C to the midpoint of an edge of the base. This follows from the fact that the medians of a triangle intersect at its centroid, and this point divides each of them in two segments, one of which is twice as long every bit the other (run into proof).

For a regular tetrahedron with side length a, radius R of its circumscribing sphere, and distances d_i from an arbitrary point in iii-space to its 4 vertices, we have^[6]

${\displaystyle {\begin{aligned}{\frac {d_{1}^{4}+d_{2}^{4}+d_{3}^{4}+d_{4}^{4}}{four}}+{\frac {16R^{four}}{9}}&=\left({\frac {d_{one}^{two}+d_{2}^{ii}+d_{iii}^{2}+d_{iv}^{2}}{four}}+{\frac {2R^{ii}}{three}}\right)^{2};\\4\left(a^{four}+d_{1}^{4}+d_{2}^{4}+d_{three}^{four}+d_{4}^{4}\right)&=\left(a^{2}+d_{ane}^{2}+d_{2}^{2}+d_{iii}^{two}+d_{four}^{ii}\right)^{2}.\end{aligned}}}$

Isometries of the regular tetrahedron [edit]

The proper rotations, (lodge-three rotation on a vertex and face, and society-2 on 2 edges) and reflection plane (through two faces and one border) in the symmetry group of the regular tetrahedron

The vertices of a cube can be grouped into two groups of four, each forming a regular tetrahedron (see above, and also animation, showing ane of the two tetrahedra in the cube). The symmetries of a regular tetrahedron stand for to one-half of those of a cube: those that map the tetrahedra to themselves, and not to each other.

The tetrahedron is the only Platonic solid that is not mapped to itself by betoken inversion.

The regular tetrahedron has 24 isometries, forming the symmetry group T_d , [3,3], (*332), isomorphic to the symmetric group, S ₄. They tin can exist categorized equally follows:

• T, [three,three]⁺, (332) is isomorphic to alternate group, A ₄ (the identity and eleven proper rotations) with the following conjugacy classes (in parentheses are given the permutations of the vertices, or correspondingly, the faces, and the unit quaternion representation):
  • identity (identity; 1)
  • rotation almost an axis through a vertex, perpendicular to the contrary plane, by an angle of ±120°: 4 axes, ii per axis, together 8 ((ane 2 3), etc.; 1 ± i ± j ± k / two )
  • rotation by an bending of 180° such that an edge maps to the opposite edge: iii ((1 ii)(iii 4), etc.; i, j, k )
• reflections in a plane perpendicular to an edge: 6
• reflections in a airplane combined with 90° rotation about an centrality perpendicular to the plane: 3 axes, 2 per axis, together half dozen; equivalently, they are xc° rotations combined with inversion (ten is mapped to −x): the rotations correspond to those of the cube about contiguous axes

Orthogonal projections of the regular tetrahedron [edit]

The regular tetrahedron has 2 special orthogonal projections, 1 centered on a vertex or equivalently on a confront, and one centered on an edge. The first corresponds to the A₂ Coxeter plane.

Orthographic projection

Centered by	Face/vertex	Edge
Image
Projective symmetry	[3]	[4]

Cantankerous department of regular tetrahedron [edit]

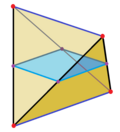
A cardinal cross section of a regular tetrahedron is a foursquare.

The ii skew perpendicular contrary edges of a regular tetrahedron define a ready of parallel planes. When i of these planes intersects the tetrahedron the resulting cross section is a rectangle.^[vii] When the intersecting plane is nigh one of the edges the rectangle is long and skinny. When halfway between the two edges the intersection is a foursquare. The aspect ratio of the rectangle reverses as yous laissez passer this halfway betoken. For the midpoint square intersection the resulting boundary line traverses every face of the tetrahedron similarly. If the tetrahedron is bisected on this plane, both halves become wedges.

A tetragonal disphenoid viewed orthogonally to the two green edges.

This property also applies for tetragonal disphenoids when applied to the two special border pairs.

Spherical tiling [edit]

The tetrahedron can also be represented every bit a spherical tiling, and projected onto the plane via a stereographic project. This projection is conformal, preserving angles just not areas or lengths. Directly lines on the sphere are projected as round arcs on the airplane.

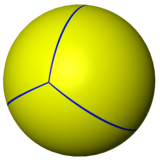Orthographic projection	Stereographic projection

Helical stacking [edit]

Regular tetrahedra can be stacked contiguous in a chiral aperiodic chain called the Boerdijk–Coxeter helix.

In four dimensions, all the convex regular iv-polytopes with tetrahedral cells (the 5-jail cell, 16-cell and 600-prison cell) can be constructed as tilings of the three-sphere by these chains, which become periodic in the three-dimensional space of the 4-polytope's purlieus surface.

Irregular tetrahedra [edit]

Tetrahedra which do not have four equilateral faces are categorized and named by the symmetries they do possess.

If all three pairs of opposite edges of a tetrahedron are perpendicular, then it is called an orthocentric tetrahedron. When just i pair of reverse edges are perpendicular, it is called a semi-orthocentric tetrahedron.

An isodynamic tetrahedron is one in which the cevians that join the vertices to the incenters of the opposite faces are concurrent.

An isogonic tetrahedron has concurrent cevians that join the vertices to the points of contact of the contrary faces with the inscribed sphere of the tetrahedron.

Trirectangular tetrahedra [edit]

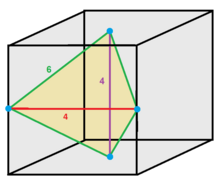
Kepler'southward drawing of a regular tetrahedron inscribed in a cube, and i of the four trirectangular tetrahedra that environment information technology, filling the cube.

In a trirectangular tetrahedron the three confront angles at one vertex are right angles, every bit at the corner of a cube.

Kepler discovered the human relationship between the cube, regular tetrahedron and trirectangular tetrahedron.^[viii]

Disphenoids [edit]

A space-filling tetrahedral disphenoid inside a cube. Two edges have dihedral angles of 90°, and 4 edges accept dihedral angles of 60°.

An isosceles tetrahedron, also called a disphenoid, is a tetrahedron where all 4 faces are coinciding acute-angled triangles, and every two edges that are opposite each other have equal lengths. The regular tetrahedron is a special case of the disphenoid (although a tetrahedron with equilateral faces is non usually called a disphenoid).

Orthoschemes [edit]

A cube dissected into 6 orthoschemes.

A three-orthoscheme is a tetrahedron where all four faces are right triangles.^[a] An orthoscheme is an irregular simplex that is the convex hull of a tree in which all edges are mutually perpendicular. In a 3-dimensional orthoscheme, the tree consists of 3 perpendicular edges connecting all 4 vertices in a linear path that makes two right-angled turns. The iii-orthoscheme is a tetrahedron having two right angles at each of two vertices, so another name for it is birectangular tetrahedron. It is also chosen a quadrirectangular tetrahedron because it contains four right angles.^[ix]

Coxeter also calls quadrirectangular tetrahedra characteristic tetrahedra, because of their integral human relationship to other polyhedra.^[10] For example, the special case of a 3-orthoscheme with equal-length perpendicular edges is the characteristic orthoscheme of the cube. If the three perpendicular edges are of unit of measurement length, its remaining edges are two of length √2 and one of length √three , so all its edges are edges or diagonals of the cube. The cube can be dissected into half dozen such 3-orthoschemes iv different ways, with all half-dozen surrounding the same √3 cube diagonal. The characteristic tetrahedron of the cube is an example of a Heronian tetrahedron.

Every regular polytope, including the regular tetrahedron, has its characteristic orthoscheme. There is an orthoscheme which is the characteristic tetrahedron of the regular tetrahedron. If the regular tetrahedron has border length 2, its characteristic orthoscheme has one edge of length 2, two edges of length one (half-edges of the regular tetrahedron), two √three edges (reverse each other), and one edge of length 1 / √2 (one of the 3 mid-border to contrary mid-edge diameters of the regular tetrahedron). The 3-orthogonal-edge path is 1, ane / √2 , 1, first forth half of one regular tetrahedron border to its mid-border, then through the center of the regular tetrahedron to its contrary mid-edge, and finally along half the opposite and perpendicular edge to the quaternary orthoscheme vertex. The regular tetrahedron can exist dissected (3 different ways) into iv such orthoschemes , which see at their common edge of length 1 / √2 .

Infinite-filling tetrahedra [edit]

A space-filling tetrahedron packs with directly congruent or enantiomorphous (mirror image) copies of itself to tile space.^[xi] The cube can be dissected into half dozen iii-orthoschemes, three left-handed and three right-handed (one of each at each cube face), and cubes can fill space, so the 3-orthoscheme is a space-filling tetrahedron in this sense.^[b] A disphenoid can be a space-filling tetrahedron in the direct congruent sense, equally in the disphenoid tetrahedral honeycomb. Regular tetrahedra, nonetheless, cannot fill space by themselves.^[c]

Fundamental domains [edit]

For Euclidean iii-infinite, there are 3 elementary and related Goursat tetrahedra. They tin be seen as points on and within a cube.

An irregular tetrahedron which is the key domain of a symmetry group is an case of a Goursat tetrahedron. The Goursat tetrahedra generate all the regular polyhedra (and many other uniform polyhedra) by mirror reflections, a procedure referred to every bit Wythoff's kaleidoscopic construction.

For polyhedra, Wythoff'due south construction arranges three mirrors at angles to each other, every bit in a kaleidoscope. Unlike a cylindrical kaleidoscope, Wythoff'due south mirrors are located at three faces of a Goursat tetrahedron such that all three mirrors intersect at a single point.^[d]

Amidst the Goursat tetrahedra which generate three-dimensional honeycombs we can recognize an orthoscheme (the characteristic tetrahedron of the cube), a double orthoscheme (the characteristic tetrahedron face-bonded to its mirror epitome), and the space-filling disphenoid illustrated in a higher place.^[x] The disphenoid is the double orthoscheme face up-bonded to its mirror image (a quadruple orthoscheme). Thus all three of these Goursat tetrahedra, and all the polyhedra they generate past reflections, can be dissected into characteristic orthoschemes of the cube.

Isometries of irregular tetrahedra [edit]

The isometries of an irregular (unmarked) tetrahedron depend on the geometry of the tetrahedron, with 7 cases possible. In each case a 3-dimensional indicate group is formed. Two other isometries (C₃, [3]⁺), and (S₄, [2⁺,4⁺]) can exist if the face or edge marking are included. Tetrahedral diagrams are included for each type below, with edges colored by isometric equivalence, and are grey colored for unique edges.

Tetrahedron name				Edge equivalence diagram	Description
Symmetry
Schön.	Cox.	Orb.	Ord.
Regular tetrahedron					Four equilateral triangles It forms the symmetry group T d, isomorphic to the symmetric group, S 4. A regular tetrahedron has Coxeter diagram and Schläfli symbol {3,iii}.
T d T	[3,3] [3,3]+	*332 332	24 12
Triangular pyramid					An equilateral triangle base and iii equal isosceles triangle sides Information technology gives half-dozen isometries, corresponding to the 6 isometries of the base. As permutations of the vertices, these 6 isometries are the identity 1, (123), (132), (12), (13) and (23), forming the symmetry group C 3v, isomorphic to the symmetric group, South 3. A triangular pyramid has Schläfli symbol {3}∨( ).
C 3v C3	[3] [iii]+	*33 33	half dozen 3
Mirrored sphenoid					Two equal scalene triangles with a common base edge This has 2 pairs of equal edges (one,3), (i,4) and (2,iii), (2,4) and otherwise no edges equal. The but two isometries are 1 and the reflection (34), giving the group C s, also isomorphic to the cyclic group, Z ii.
C s =C 1h =C 1v	[ ]	*	2
Irregular tetrahedron (No symmetry)					Four unequal triangles Its but isometry is the identity, and the symmetry group is the trivial group. An irregular tetrahedron has Schläfli symbol ( )∨( )∨( )∨( ).
C1	[ ]+	1	1
Disphenoids (4 equal triangles)
Tetragonal disphenoid					Four equal isosceles triangles It has 8 isometries. If edges (ane,two) and (3,four) are of different length to the other 4 so the 8 isometries are the identity ane, reflections (12) and (34), and 180° rotations (12)(34), (thirteen)(24), (xiv)(23) and improper ninety° rotations (1234) and (1432) forming the symmetry group D 2d. A tetragonal disphenoid has Coxeter diagram and Schläfli symbol s{2,iv}.
D 2d S4	[2+,4] [2+,4+]	2*2 two×	8 4
Rhombic disphenoid					4 equal scalene triangles It has iv isometries. The isometries are i and the 180° rotations (12)(34), (13)(24), (xiv)(23). This is the Klein four-group 5 4 or Z 2 ii, nowadays equally the signal group D 2. A rhombic disphenoid has Coxeter diagram and Schläfli symbol sr{2,2}.
D two	[ii,ii]+	222	4
Generalized disphenoids (two pairs of equal triangles)
Digonal disphenoid					Two pairs of equal isosceles triangles This gives two opposite edges (one,2) and (iii,4) that are perpendicular but different lengths, and then the 4 isometries are one, reflections (12) and (34) and the 180° rotation (12)(34). The symmetry group is C 2v, isomorphic to the Klein four-group V iv. A digonal disphenoid has Schläfli symbol { }∨{ }.
C 2v C two	[ii] [ii]+	*22 22	4 2
Phyllic disphenoid					Two pairs of equal scalene or isosceles triangles This has two pairs of equal edges (1,3), (2,4) and (i,4), (two,three) just otherwise no edges equal. The only 2 isometries are 1 and the rotation (12)(34), giving the group C 2 isomorphic to the cyclic group, Z ii.
C ii	[two]+	22	2

General properties [edit]

Volume [edit]

The volume of a tetrahedron is given by the pyramid volume formula:

${\displaystyle V={\frac {i}{3}}A_{0}\,h\,}$

where A ₀ is the area of the base and h is the elevation from the base to the noon. This applies for each of the four choices of the base, so the distances from the apexes to the opposite faces are inversely proportional to the areas of these faces.

For a tetrahedron with vertices a = (a ₁, a ₂, a _three), b = (b _ane, b _two, b ₃), c = (c _i, c ₂, c _iii), and d = (d ₁, d ₂, d ₃), the volume is 1 / 6 |det(a − d, b − d, c − d)|, or whatever other combination of pairs of vertices that form a simply continued graph. This can be rewritten using a dot production and a cross product, yielding

${\displaystyle V={\frac {|(\mathbf {a} -\mathbf {d} )\cdot ((\mathbf {b} -\mathbf {d} )\times (\mathbf {c} -\mathbf {d} ))|}{half dozen}}.}$

If the origin of the coordinate system is called to coincide with vertex d, so d = 0, then

${\displaystyle V={\frac {|\mathbf {a} \cdot (\mathbf {b} \times \mathbf {c} )|}{6}},}$

where a, b, and c represent three edges that meet at i vertex, and a · (b × c) is a scalar triple product. Comparison this formula with that used to compute the volume of a parallelepiped, nosotros conclude that the book of a tetrahedron is equal to i / 6 of the book of whatever parallelepiped that shares three converging edges with it.

The absolute value of the scalar triple product tin can be represented as the following absolute values of determinants:

${\displaystyle six\cdot V={\begin{Vmatrix}\mathbf {a} &\mathbf {b} &\mathbf {c} \end{Vmatrix}}}$ or ${\displaystyle 6\cdot 5={\begin{Vmatrix}\mathbf {a} \\\mathbf {b} \\\mathbf {c} \cease{Vmatrix}}}$ where ${\displaystyle {\begin{cases}\mathbf {a} =(a_{one},a_{2},a_{three}),\\\mathbf {b} =(b_{i},b_{two},b_{3}),\\\mathbf {c} =(c_{ane},c_{2},c_{iii}),\terminate{cases}}}$ are expressed as row or column vectors.

Hence

${\displaystyle 36\cdot V^{ii}={\begin{vmatrix}\mathbf {a^{2}} &\mathbf {a} \cdot \mathbf {b} &\mathbf {a} \cdot \mathbf {c} \\\mathbf {a} \cdot \mathbf {b} &\mathbf {b^{2}} &\mathbf {b} \cdot \mathbf {c} \\\mathbf {a} \cdot \mathbf {c} &\mathbf {b} \cdot \mathbf {c} &\mathbf {c^{2}} \cease{vmatrix}}}$ where ${\displaystyle {\begin{cases}\mathbf {a} \cdot \mathbf {b} =ab\cos {\gamma },\\\mathbf {b} \cdot \mathbf {c} =bc\cos {\alpha },\\\mathbf {a} \cdot \mathbf {c} =ac\cos {\beta }.\end{cases}}}$

which gives

${\displaystyle 5={\frac {abc}{6}}{\sqrt {1+ii\cos {\alpha }\cos {\beta }\cos {\gamma }-\cos ^{two}{\blastoff }-\cos ^{two}{\beta }-\cos ^{2}{\gamma }}},\,}$

where α, β, γ are the plane angles occurring in vertex d. The angle α, is the angle between the ii edges connecting the vertex d to the vertices b and c. The angle β, does so for the vertices a and c, while γ, is defined by the position of the vertices a and b.

If we exercise not require that d = 0 and then

${\displaystyle 6\cdot V=\left|\det \left({\begin{matrix}a_{1}&b_{ane}&c_{1}&d_{1}\\a_{ii}&b_{ii}&c_{two}&d_{two}\\a_{three}&b_{3}&c_{3}&d_{3}\\1&1&i&1\stop{matrix}}\right)\right|\,.}$

Given the distances between the vertices of a tetrahedron the volume can be computed using the Cayley–Menger determinant:

${\displaystyle 288\cdot V^{two}={\brainstorm{vmatrix}0&1&1&1&1\\ane&0&d_{12}^{2}&d_{13}^{2}&d_{fourteen}^{ii}\\ane&d_{12}^{2}&0&d_{23}^{2}&d_{24}^{ii}\\1&d_{13}^{two}&d_{23}^{two}&0&d_{34}^{ii}\\i&d_{14}^{two}&d_{24}^{ii}&d_{34}^{2}&0\end{vmatrix}}}$

where the subscripts i, j ∈ {1, ii, 3, 4} stand for the vertices {a, b, c, d} and d_ij is the pairwise distance betwixt them – i.e., the length of the border connecting the ii vertices. A negative value of the determinant means that a tetrahedron cannot be synthetic with the given distances. This formula, sometimes chosen Tartaglia's formula, is essentially due to the painter Piero della Francesca in the 15th century, every bit a 3 dimensional analogue of the 1st century Heron'south formula for the expanse of a triangle.^[12]

Denote a, b, c be 3 edges that encounter at a bespeak, and 10, y, z the contrary edges. Allow V be the volume of the tetrahedron; then^[13]

${\displaystyle V={\frac {\sqrt {4a^{ii}b^{two}c^{two}-a^{2}X^{2}-b^{2}Y^{2}-c^{2}Z^{2}+XYZ}}{12}}}$

where

${\displaystyle {\begin{aligned}10&=b^{ii}+c^{2}-x^{ii},\\Y&=a^{ii}+c^{ii}-y^{2},\\Z&=a^{ii}+b^{two}-z^{2}.\stop{aligned}}}$

The above formula uses six lengths of edges, and the post-obit formula uses three lengths of edges and three angles.

${\displaystyle Five={\frac {abc}{6}}{\sqrt {1+2\cos {\alpha }\cos {\beta }\cos {\gamma }-\cos ^{two}{\alpha }-\cos ^{2}{\beta }-\cos ^{2}{\gamma }}}}$

Heron-type formula for the volume of a tetrahedron [edit]

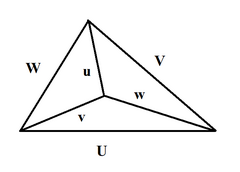
Vi edge-lengths of Tetrahedron

If U, V, W, u, 5, west are lengths of edges of the tetrahedron (first 3 form a triangle; u opposite to U then on), so^[14]

${\displaystyle V={\frac {\sqrt {\,(-p+q+r+s)\,(p-q+r+southward)\,(p+q-r+s)\,(p+q+r-s)}}{192\,u\,v\,w}}}$

where

${\displaystyle {\begin{aligned}p&={\sqrt {xYZ}},&q&={\sqrt {yZX}},&r&={\sqrt {zXY}},&s&={\sqrt {xyz}},\end{aligned}}}$

${\displaystyle {\begin{aligned}Ten&=(w-U+5)\,(U+v+w),&x&=(U-v+west)\,(v-w+U),\\Y&=(u-Five+due west)\,(5+w+u),&y&=(Five-w+u)\,(w-u+V),\\Z&=(v-W+u)\,(Due west+u+v),&z&=(W-u+v)\,(u-v+W).\cease{aligned}}}$

Book divider [edit]

Any aeroplane containing a bimedian (connector of contrary edges' midpoints) of a tetrahedron bisects the volume of the tetrahedron.^[15]

Non-Euclidean book [edit]

For tetrahedra in hyperbolic space or in iii-dimensional elliptic geometry, the dihedral angles of the tetrahedron make up one's mind its shape and hence its volume. In these cases, the volume is given past the Murakami–Yano formula.^[sixteen] Yet, in Euclidean space, scaling a tetrahedron changes its volume but not its dihedral angles, and then no such formula tin can exist.

Distance between the edges [edit]

Any two reverse edges of a tetrahedron lie on two skew lines, and the altitude betwixt the edges is divers as the distance between the two skew lines. Let d be the distance between the skew lines formed by opposite edges a and b − c as calculated here. And then another volume formula is given past

${\displaystyle V={\frac {d|(\mathbf {a} \times \mathbf {(b-c)} )|}{6}}.}$

Backdrop analogous to those of a triangle [edit]

The tetrahedron has many backdrop analogous to those of a triangle, including an insphere, circumsphere, medial tetrahedron, and exspheres. It has respective centers such every bit incenter, circumcenter, excenters, Spieker centre and points such every bit a centroid. Yet, at that place is by and large no orthocenter in the sense of intersecting altitudes.^[17]

Gaspard Monge plant a eye that exists in every tetrahedron, at present known equally the Monge signal: the point where the half-dozen midplanes of a tetrahedron intersect. A midplane is divers every bit a aeroplane that is orthogonal to an border joining any 2 vertices that besides contains the centroid of an contrary edge formed past joining the other two vertices. If the tetrahedron'due south altitudes exercise intersect, then the Monge signal and the orthocenter coincide to give the class of orthocentric tetrahedron.

An orthogonal line dropped from the Monge point to any face meets that face at the midpoint of the line segment between that face's orthocenter and the foot of the distance dropped from the opposite vertex.

A line segment joining a vertex of a tetrahedron with the centroid of the reverse face is called a median and a line segment joining the midpoints of ii opposite edges is chosen a bimedian of the tetrahedron. Hence there are four medians and three bimedians in a tetrahedron. These seven line segments are all concurrent at a point called the centroid of the tetrahedron.^[xviii] In addition the four medians are divided in a 3:1 ratio by the centroid (see Commandino'southward theorem). The centroid of a tetrahedron is the midpoint between its Monge point and circumcenter. These points ascertain the Euler line of the tetrahedron that is analogous to the Euler line of a triangle.

The nine-point circle of the general triangle has an analogue in the circumsphere of a tetrahedron'due south medial tetrahedron. It is the twelve-point sphere and as well the centroids of the iv faces of the reference tetrahedron, it passes through four substitute Euler points, one tertiary of the way from the Monge point toward each of the four vertices. Finally it passes through the iv base points of orthogonal lines dropped from each Euler point to the confront not containing the vertex that generated the Euler point.^[nineteen]

The center T of the twelve-point sphere also lies on the Euler line. Unlike its triangular counterpart, this middle lies one third of the way from the Monge signal One thousand towards the circumcenter. Also, an orthogonal line through T to a called face is coplanar with two other orthogonal lines to the same face. The first is an orthogonal line passing through the corresponding Euler bespeak to the chosen face. The second is an orthogonal line passing through the centroid of the chosen face. This orthogonal line through the twelve-betoken center lies midway between the Euler indicate orthogonal line and the centroidal orthogonal line. Furthermore, for whatever face, the twelve-signal center lies at the midpoint of the corresponding Euler indicate and the orthocenter for that face.

The radius of the twelve-signal sphere is 1 third of the circumradius of the reference tetrahedron.

There is a relation among the angles made by the faces of a full general tetrahedron given by^[20]

${\displaystyle {\begin{vmatrix}-one&\cos {(\alpha _{12})}&\cos {(\alpha _{thirteen})}&\cos {(\blastoff _{xiv})}\\\cos {(\alpha _{12})}&-ane&\cos {(\alpha _{23})}&\cos {(\alpha _{24})}\\\cos {(\alpha _{13})}&\cos {(\blastoff _{23})}&-1&\cos {(\alpha _{34})}\\\cos {(\alpha _{14})}&\cos {(\blastoff _{24})}&\cos {(\alpha _{34})}&-ane\\\end{vmatrix}}=0\,}$

where α_ij is the angle between the faces i and j.

The geometric median of the vertex position coordinates of a tetrahedron and its isogonic center are associated, nether circumstances analogous to those observed for a triangle. Lorenz Lindelöf institute that, corresponding to whatever given tetrahedron is a point at present known as an isogonic middle, O, at which the solid angles subtended past the faces are equal, having a mutual value of π sr, and at which the angles subtended by reverse edges are equal.^[21] A solid bending of π sr is one quarter of that subtended by all of space. When all the solid angles at the vertices of a tetrahedron are smaller than π sr, O lies inside the tetrahedron, and because the sum of distances from O to the vertices is a minimum, O coincides with the geometric median, M, of the vertices. In the event that the solid angle at one of the vertices, five, measures exactly π sr, then O and M coincide with v. If however, a tetrahedron has a vertex, five, with solid bending greater than π sr, Grand withal corresponds to five, but O lies exterior the tetrahedron.

Geometric relations [edit]

A tetrahedron is a 3-simplex. Dissimilar the case of the other Platonic solids, all the vertices of a regular tetrahedron are equidistant from each other (they are the only possible arrangement of four equidistant points in iii-dimensional space).

A tetrahedron is a triangular pyramid, and the regular tetrahedron is self-dual.

A regular tetrahedron can be embedded within a cube in two means such that each vertex is a vertex of the cube, and each border is a diagonal of one of the cube'southward faces. For i such embedding, the Cartesian coordinates of the vertices are

(+1, +1, +1);

(−1, −one, +1);

(−1, +ane, −i);

(+1, −ane, −1).

This yields a tetrahedron with edge-length 2√2 , centered at the origin. For the other tetrahedron (which is dual to the first), reverse all the signs. These 2 tetrahedra's vertices combined are the vertices of a cube, demonstrating that the regular tetrahedron is the 3-demicube.

The book of this tetrahedron is one-third the volume of the cube. Combining both tetrahedra gives a regular polyhedral compound chosen the chemical compound of two tetrahedra or stella octangula.

The interior of the stella octangula is an octahedron, and correspondingly, a regular octahedron is the result of cutting off, from a regular tetrahedron, 4 regular tetrahedra of half the linear size (i.east., rectifying the tetrahedron).

The to a higher place embedding divides the cube into five tetrahedra, one of which is regular. In fact, five is the minimum number of tetrahedra required to etch a cube. To encounter this, starting from a base tetrahedron with 4 vertices, each added tetrahedra adds at most 1 new vertex, so at least 4 more must be added to make a cube, which has viii vertices.

Inscribing tetrahedra inside the regular compound of 5 cubes gives two more regular compounds, containing five and ten tetrahedra.

Regular tetrahedra cannot tessellate space by themselves, although this result seems likely plenty that Aristotle claimed it was possible. Even so, two regular tetrahedra tin can be combined with an octahedron, giving a rhombohedron that can tile infinite as the tetrahedral-octahedral honeycomb.

However, several irregular tetrahedra are known, of which copies can tile infinite, for instance the feature orthoscheme of the cube and the disphenoid of the disphenoid tetrahedral honeycomb. The complete listing remains an open problem.^[22]

If one relaxes the requirement that the tetrahedra be all the same shape, i can tile space using but tetrahedra in many different ways. For example, one can separate an octahedron into iv identical tetrahedra and combine them again with 2 regular ones. (As a side-note: these two kinds of tetrahedron have the same volume.)

The tetrahedron is unique among the uniform polyhedra in possessing no parallel faces.

A law of sines for tetrahedra and the infinite of all shapes of tetrahedra [edit]

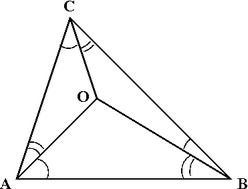
A corollary of the usual law of sines is that in a tetrahedron with vertices O, A, B, C, nosotros accept

${\displaystyle \sin \bending OAB\cdot \sin \angle OBC\cdot \sin \angle OCA=\sin \angle OAC\cdot \sin \bending OCB\cdot \sin \bending OBA.\,}$

One may view the 2 sides of this identity every bit corresponding to clockwise and counterclockwise orientations of the surface.

Putting any of the 4 vertices in the role of O yields four such identities, but at almost 3 of them are independent: If the "clockwise" sides of 3 of them are multiplied and the product is inferred to exist equal to the production of the "counterclockwise" sides of the same three identities, and and then common factors are cancelled from both sides, the event is the quaternary identity.

Three angles are the angles of some triangle if and only if their sum is 180° (π radians). What condition on 12 angles is necessary and sufficient for them to be the 12 angles of some tetrahedron? Clearly the sum of the angles of any side of the tetrahedron must be 180°. Since in that location are iv such triangles, there are four such constraints on sums of angles, and the number of degrees of freedom is thereby reduced from 12 to 8. The 4 relations given by this sine law further reduce the number of degrees of freedom, from 8 down to not 4 but 5, since the fourth constraint is non contained of the offset 3. Thus the infinite of all shapes of tetrahedra is five-dimensional.^[23]

Law of cosines for tetrahedra [edit]

Let {P ₁ ,P ₂, P ₃, P ₄} be the points of a tetrahedron. Permit Δ _i be the area of the face opposite vertex P_i and let θ_ij be the dihedral angle betwixt the two faces of the tetrahedron adjacent to the edge P_iP_j .

The law of cosines for this tetrahedron,^[24] which relates the areas of the faces of the tetrahedron to the dihedral angles about a vertex, is given by the following relation:

${\displaystyle \Delta _{i}^{2}=\Delta _{j}^{two}+\Delta _{thou}^{two}+\Delta _{l}^{2}-2(\Delta _{j}\Delta _{one thousand}\cos \theta _{il}+\Delta _{j}\Delta _{l}\cos \theta _{ik}+\Delta _{k}\Delta _{50}\cos \theta _{ij})}$

Interior point [edit]

Let P be any interior bespeak of a tetrahedron of volume Five for which the vertices are A, B, C, and D, and for which the areas of the opposite faces are F _a, F _b, F _c, and F _d. And so^{[25] : p.62, #1609}

${\displaystyle PA\cdot F_{\mathrm {a} }+Atomic number 82\cdot F_{\mathrm {b} }+PC\cdot F_{\mathrm {c} }+PD\cdot F_{\mathrm {d} }\geq 9V.}$

For vertices A, B, C, and D, interior signal P, and feet J, K, L, and K of the perpendiculars from P to the faces, and suppose the faces have equal areas, then^{[25] : p.226, #215}

${\displaystyle PA+Pb+PC+PD\geq 3(PJ+PK+PL+PM).}$

Inradius [edit]

Denoting the inradius of a tetrahedron as r and the inradii of its triangular faces equally r _i for i = 1, 2, 3, 4, we have^{[25] : p.81, #1990}

${\displaystyle {\frac {ane}{r_{1}^{2}}}+{\frac {ane}{r_{2}^{two}}}+{\frac {1}{r_{3}^{ii}}}+{\frac {1}{r_{4}^{ii}}}\leq {\frac {two}{r^{2}}},}$

with equality if and only if the tetrahedron is regular.

If A _ane , A ₂ , A _iii and A ₄ denote the area of each faces, the value of r is given by

${\displaystyle r={\frac {3V}{A_{i}+A_{2}+A_{3}+A_{four}}}}$ .

This formula is obtained from dividing the tetrahedron into iv tetrahedra whose points are the three points of 1 of the original faces and the incenter. Since the iv subtetrahedra fill the volume, we accept ${\displaystyle V={\frac {one}{3}}A_{ane}r+{\frac {1}{3}}A_{ii}r+{\frac {1}{3}}A_{3}r+{\frac {1}{3}}A_{four}r}$ .

Circumradius [edit]

Denote the circumradius of a tetrahedron equally R. Allow a, b, c exist the lengths of the three edges that meet at a vertex, and A, B, C the length of the opposite edges. Let V be the book of the tetrahedron. Then^{[26] [27]}

${\displaystyle R={\frac {\sqrt {(aA+bB+cC)(aA+bB-cC)(aA-bB+cC)(-aA+bB+cC)}}{24V}}.}$

Circumcenter [edit]

The circumcenter of a tetrahedron can be found as intersection of three bisector planes. A bisector plane is defined as the aeroplane centered on, and orthogonal to an edge of the tetrahedron. With this definition, the circumcenter C of a tetrahedron with vertices x ₀ , 10 ₁ , x ₂ , x ₃ can be formulated as matrix-vector production:^[28]

${\displaystyle {\begin{aligned}C&=A^{-1}B&{\text{where}}&\ &A=\left({\begin{matrix}\left[x_{1}-x_{0}\right]^{T}\\\left[x_{2}-x_{0}\correct]^{T}\\\left[x_{three}-x_{0}\right]^{T}\end{matrix}}\correct)&\ &{\text{and}}&\ &B={\frac {1}{2}}\left({\begin{matrix}\|x_{one}\|^{2}-\|x_{0}\|^{2}\\\|x_{ii}\|^{2}-\|x_{0}\|^{two}\\\|x_{3}\|^{2}-\|x_{0}\|^{ii}\end{matrix}}\correct)\\\end{aligned}}}$

In dissimilarity to the centroid, the circumcenter may not always lay on the inside of a tetrahedron. Analogously to an obtuse triangle, the circumcenter is outside of the object for an obtuse tetrahedron.

Centroid [edit]

The tetrahedron's center of mass computes as the arithmetic mean of its four vertices, see Centroid.

Faces [edit]

The sum of the areas of any three faces is greater than the surface area of the 4th face.^{[25] : p.225, #159}

Integer tetrahedra [edit]

In that location exist tetrahedra having integer-valued edge lengths, confront areas and volume. These are called Heronian tetrahedra. One example has 1 edge of 896, the opposite edge of 990 and the other four edges of 1073; ii faces are isosceles triangles with areas of 436800 and the other two are isosceles with areas of 47120 , while the volume is 124185 600 .^[29]

A tetrahedron can have integer volume and sequent integers as edges, an example being the one with edges half-dozen, seven, 8, 9, 10, and 11 and volume 48.^[30]

Related polyhedra and compounds [edit]

A regular tetrahedron tin be seen as a triangular pyramid.

Regular pyramids
Digonal	Triangular	Square	Pentagonal	Hexagonal	Heptagonal	Octagonal	Enneagonal	Decagonal...
Improper	Regular	Equilateral		Isosceles

A regular tetrahedron can exist seen as a degenerate polyhedron, a uniform digonal antiprism, where base polygons are reduced digons.

Family unit of uniform n-gonal antiprisms

• v
• t
• e

Antiprism name	Digonal antiprism	(Trigonal) Triangular antiprism	(Tetragonal) Square antiprism	Pentagonal antiprism	Hexagonal antiprism	Heptagonal antiprism	Octagonal antiprism	Enneagonal antiprism	Decagonal antiprism	Hendecagonal antiprism	Dodecagonal antiprism	...	Apeirogonal antiprism
Polyhedron image												...
Spherical tiling prototype												Aeroplane tiling image
Vertex config.	2.three.3.iii	3.3.3.3	4.3.3.iii	five.iii.3.3	6.iii.3.3	7.3.3.three	8.iii.iii.3	nine.3.3.3	x.3.iii.3	11.3.3.3	12.3.3.3	...	∞.3.3.three

A regular tetrahedron can be seen equally a degenerate polyhedron, a uniform dual digonal trapezohedron, containing vi vertices, in two sets of colinear edges.

Family unit of n-gonal trapezohedra

Trapezohedron proper name	Digonal trapezohedron (Tetrahedron)	Trigonal trapezohedron	Tetragonal trapezohedron	Pentagonal trapezohedron	Hexagonal trapezohedron	Heptagonal trapezohedron	Octagonal trapezohedron	Decagonal trapezohedron	Dodecagonal trapezohedron	...	Apeirogonal trapezohedron
Polyhedron image										...
Spherical tiling image										Plane tiling image
Face configuration	V2.3.3.3	V3.3.3.3	V4.three.3.iii	V5.3.3.3	V6.3.three.3	V7.3.three.3	V8.3.3.3	V10.3.3.3	V12.3.3.3	...	V∞.3.3.3

A truncation procedure applied to the tetrahedron produces a series of uniform polyhedra. Truncating edges down to points produces the octahedron every bit a rectified tetrahedron. The process completes as a birectification, reducing the original faces down to points, and producing the self-dual tetrahedron once over again.

Family of compatible tetrahedral polyhedra
Symmetry: [three,3], (*332)							[3,3]+, (332)
{3,3}	t{three,iii}	r{iii,3}	t{3,3}	{3,iii}	rr{3,iii}	tr{three,3}	sr{3,3}
Duals to uniform polyhedra
V3.iii.3	V3.6.half-dozen	V3.iii.3.three	V3.6.6	V3.3.3	V3.iv.3.4	V4.6.6	V3.3.three.3.3

This polyhedron is topologically related equally a part of sequence of regular polyhedra with Schläfli symbols {iii,due north}, continuing into the hyperbolic aeroplane.

*n32 symmetry mutation of regular tilings: {3,n} v t e
Spherical				Euclid.	Compact hyper.		Paraco.	Noncompact hyperbolic
3.three	33	34	three5	3vi	3vii	iiieight	3∞	three12i	three9i	36i	33i

The tetrahedron is topologically related to a serial of regular polyhedra and tilings with social club-3 vertex figures.

*n32 symmetry mutation of regular tilings: {north,3} v t due east
Spherical				Euclidean	Compact hyperb.		Paraco.	Noncompact hyperbolic
{2,three}	{iii,3}	{4,iii}	{v,3}	{6,3}	{vii,3}	{8,3}	{∞,3}	{12i,3}	{9i,3}	{6i,3}	{3i,3}

• Compounds of tetrahedra

• 

• 

• 

An interesting polyhedron tin be constructed from five intersecting tetrahedra. This compound of 5 tetrahedra has been known for hundreds of years. It comes upward regularly in the earth of origami. Joining the twenty vertices would form a regular dodecahedron. There are both left-handed and correct-handed forms, which are mirror images of each other. Superimposing both forms gives a compound of ten tetrahedra, in which the ten tetrahedra are arranged as five pairs of stellae octangulae. A stella octangula is a chemical compound of two tetrahedra in dual position and its 8 vertices define a cube as their convex hull.

The square hosohedron is another polyhedron with 4 faces, but information technology does not take triangular faces.

The Szilassi polyhedron and the tetrahedron are the merely 2 known polyhedra in which each face up shares an edge with each other face.

Applications [edit]

Numerical assay [edit]

An irregular volume in space can exist approximated by an irregular triangulated surface, and irregular tetrahedral volume elements.

In numerical analysis, complicated three-dimensional shapes are commonly broken downward into, or approximated by, a polygonal mesh of irregular tetrahedra in the procedure of setting up the equations for finite chemical element analysis peculiarly in the numerical solution of partial differential equations. These methods have wide applications in practical applications in computational fluid dynamics, aerodynamics, electromagnetic fields, civil technology, chemical engineering, naval compages and engineering, and related fields.

Structural applied science [edit]

A tetrahedron having potent edges is inherently rigid. For this reason it is often used to stiffen frame structures such as spaceframes.

Aviation [edit]

At some airfields, a large frame in the shape of a tetrahedron with two sides covered with a thin textile is mounted on a rotating pivot and always points into the air current. It is congenital large enough to be seen from the air and is sometimes illuminated. Its purpose is to serve as a reference to pilots indicating wind management.^[31]

Chemistry [edit]

The tetrahedron shape is seen in nature in covalently bonded molecules. All sp³-hybridized atoms are surrounded past atoms (or alone electron pairs) at the iv corners of a tetrahedron. For example in a methane molecule (CH
₄ ) or an ammonium ion (NH ⁺
₄ ), four hydrogen atoms environment a central carbon or nitrogen atom with tetrahedral symmetry. For this reason, one of the leading journals in organic chemistry is called Tetrahedron. The cardinal bending between any 2 vertices of a perfect tetrahedron is arccos(− one / 3 ), or approximately 109.47°.^[five]

Water, H
₂ O, also has a tetrahedral structure, with two hydrogen atoms and two lone pairs of electrons around the fundamental oxygen atoms. Its tetrahedral symmetry is not perfect, however, because the solitary pairs repel more than the single O–H bonds.

4th phase diagrams of mixtures of chemical substances are represented graphically as tetrahedra.

Yet, 4th phase diagrams in communication applied science are represented graphically on a two-dimensional plane.

Electricity and electronics [edit]

If six equal resistors are soldered together to form a tetrahedron, then the resistance measured between whatsoever two vertices is half that of one resistor.^{[32] [33]}

Since silicon is the most common semiconductor used in solid-country electronics, and silicon has a valence of four, the tetrahedral shape of the four chemical bonds in silicon is a potent influence on how crystals of silicon form and what shapes they assume.

Color space [edit]

Tetrahedra are used in color space conversion algorithms specifically for cases in which the luminance axis diagonally segments the colour space (east.g. RGB, CMY).^[34]

Games [edit]

The Royal Game of Ur, dating from 2600 BC, was played with a set of tetrahedral dice.

Especially in roleplaying, this solid is known equally a 4-sided dice, ane of the more common polyhedral dice, with the number rolled appearing around the bottom or on the top vertex. Some Rubik'southward Cube-like puzzles are tetrahedral, such as the Pyraminx and Pyramorphix.

Geology [edit]

The tetrahedral hypothesis, originally published by William Lowthian Dark-green to explain the germination of the Globe,^[35] was popular through the early 20th century.^{[36] [37]}

Weaponry [edit]

Modern caltrop with hollow spikes to puncture self-sealing rubber tyres

Some caltrops are based on tetrahedra equally one spike points upwards regardless of how they state and tin be easily made past welding two bent nails together.

Contemporary art [edit]

The Austrian artist Martina Schettina created a tetrahedron using fluorescent lamps. It was shown at the calorie-free art biennale Austria 2010.^[38]

It is used equally album artwork, surrounded by black flames on The End of All Things to Come up by Mudvayne.

Popular civilization [edit]

Stanley Kubrick originally intended the monolith in 2001: A Space Odyssey to be a tetrahedron, according to Marvin Minsky, a cognitive scientist and expert on bogus intelligence who advised Kubrick on the HAL 9000 computer and other aspects of the movie. Kubrick scrapped the thought of using the tetrahedron every bit a company who saw footage of it did not recognize what information technology was and he did not want anything in the picture show regular people did non understand.^[39]

In Season half-dozen, Episode fifteen of Futurama, named "Möbius Dick", the Planet Limited crew laissez passer through an area in space known as the Bermuda Tetrahedron. Many other ships passing through the area have mysteriously disappeared, including that of the first Planet Limited coiffure.

In the 2013 picture show Oblivion the large construction in orbit above the Earth is of a tetrahedron pattern and referred to as the Tet.

Tetrahedral graph [edit]

Tetrahedral graph
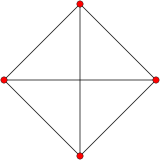Vertices	iv
Edges	6
Radius	1
Diameter	1
Girth	3
Automorphisms	24
Chromatic number	4
Backdrop	Hamiltonian, regular, symmetric, distance-regular, distance-transitive, iii-vertex-connected, planar graph
Table of graphs and parameters

The skeleton of the tetrahedron (comprising the vertices and edges) forms a graph, with 4 vertices, and six edges. It is a special case of the complete graph, Chiliad₄, and bicycle graph, W₄.^[40] Information technology is 1 of five Platonic graphs, each a skeleton of its Platonic solid.

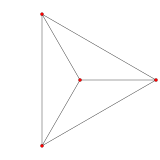
iii-fold symmetry

Run across likewise [edit]

• Boerdijk–Coxeter helix
• Möbius configuration
• Caltrop
• Demihypercube and simplex – n-dimensional analogues
• Pentachoron – 4-dimensional analogue
• Synergetics (Fuller)
• Tetrahedral kite
• Tetrahedral number
• Tetrahedron packing
• Triangular dipyramid – synthetic past joining ii tetrahedra along one face
• Trirectangular tetrahedron
• Orthoscheme

Notes [edit]

1. ^ A 3-orthoscheme is not a disphenoid, considering its opposite edges are non of equal length. Information technology is not possible to construct a disphenoid with correct triangle or obtuse triangle faces.
2. ^ The characteristic orthoscheme of the cube is ane of the Colina tetrahedra, a family of infinite-filling tetrahedra. All space-filling tetrahedra are pair of scissors-coinciding to a cube. Every convex polyhedron is scissors-congruent to an orthoscheme.
3. ^ The tetrahedral-octahedral honeycomb fills space with alternating regular tetrahedron cells and regular octahedron cells in a ratio of ii:i.
4. ^ The Coxeter-Dynkin diagram of the generated polyhedron contains three nodes representing the three mirrors. The dihedral angle between each pair of mirrors is encoded in the diagram, as well as the location of a unmarried generating indicate which is multiplied past mirror reflections into the vertices of the polyhedron. For a regular polyhedron, the Coxeter-Dynkin diagram of the generating feature orthoscheme is the generated polyhedron'southward diagram without the generating point marking.

References [edit]

1. ^ ^{a b} Weisstein, Eric Due west. "Tetrahedron". MathWorld.
2. ^ Ford, Walter Burton; Ammerman, Charles (1913), Plane and Solid Geometry, Macmillan, pp. 294–295
3. ^ ^{a b c d e f} Coxeter, Harold Scott MacDonald; Regular Polytopes, Methuen and Co., 1948, Table I(i)
4. ^ Köller, Jürgen, "Tetrahedron", Mathematische Basteleien, 2001
5. ^ ^{a b} Brittin, Westward. Due east. (1945). "Valence bending of the tetrahedral carbon atom". Journal of Chemical Didactics. 22 (3): 145. Bibcode:1945JChEd..22..145B. doi:x.1021/ed022p145.
6. ^ Park, Poo-Sung. "Regular polytope distances", Forum Geometricorum 16, 2016, 227–232. http://forumgeom.fau.edu/FG2016volume16/FG201627.pdf
7. ^ "Sections of a Tetrahedron".
8. ^ Kepler 1619, p. 181.
9. ^ Coxeter, H.Due south.M. (1989). "Trisecting an Orthoscheme". Computers Math. Applic. 17 (1–3): 59–71.
10. ^ ^{a b} Coxeter 1973, pp. 71–72, §4.7 Characteristic tetrahedra.
11. ^ Coxeter 1973, pp. 33–34, §3.one Congruent transformations.
12. ^ "Simplex Volumes and the Cayley-Menger Determinant", MathPages.com
13. ^ Kahan, William Chiliad. (three Apr 2012), What has the Volume of a Tetrahedron to do with Estimator Programming Languages? (PDF), p. xi
14. ^ Kahan, William M. (3 April 2012), What has the Volume of a Tetrahedron to exercise with Computer Programming Languages? (PDF), pp. 16–17
15. ^ Bottema, O. "A Theorem of Bobillier on the Tetrahedron." Elemente der Mathematik 24 (1969): six-10.
16. ^ Murakami, Jun; Yano, Masakazu (2005), "On the volume of a hyperbolic and spherical tetrahedron", Communications in Analysis and Geometry, 13 (ii): 379–400, doi:10.4310/cag.2005.v13.n2.a5, ISSN 1019-8385, MR 2154824
17. ^ Havlicek, Hans; Weiß, Gunter (2003). "Altitudes of a tetrahedron and traceless quadratic forms" (PDF). American Mathematical Monthly. 110 (8): 679–693. arXiv:1304.0179. doi:ten.2307/3647851. JSTOR 3647851.
18. ^ Leung, Kam-tim; and Suen, Suk-nam; "Vectors, matrices and geometry", Hong Kong University Press, 1994, pp. 53–54
19. ^ Outudee, Somluck; New, Stephen. The Diverse Kinds of Centres of Simplices (PDF). Dept of Mathematics, Chulalongkorn Academy, Bangkok. Archived from the original on 27 February 2009. {{cite volume}}: CS1 maint: bot: original URL status unknown (link)
20. ^ Audet, Daniel (May 2011). "Déterminants sphérique et hyperbolique de Cayley-Menger" (PDF). Bulletin AMQ.
21. ^ Lindelof, L. (1867). "Sur les maxima et minima d'une fonction des rayons vecteurs menés d'un point mobile à plusieurs centres fixes". Acta Societatis Scientiarum Fennicae. 8 (Role 1): 189–203.
22. ^ Senechal, Marjorie (1981). "Which tetrahedra fill space?". Mathematics Magazine. Mathematical Association of America. 54 (5): 227–243. doi:ten.2307/2689983. JSTOR 2689983.
23. ^ Rassat, André; Fowler, Patrick W. (2004). "Is There a "Most Chiral Tetrahedron"?". Chemistry: A European Journal. 10 (24): 6575–6580. doi:10.1002/chem.200400869. PMID 15558830.
24. ^ Lee, Jung Rye (June 1997). "The Police of Cosines in a Tetrahedron". J. Korea Soc. Math. Educ. Ser. B: Pure Appl. Math.
25. ^ ^{a b c d} Inequalities proposed in "Crux Mathematicorum", [i].
26. ^ Crelle, A. L. (1821). "Einige Bemerkungen über die dreiseitige Pyramide". Sammlung mathematischer Aufsätze u. Bemerkungen 1 (in German). Berlin: Maurer. pp. 105–132. Retrieved 7 August 2018.
27. ^ Todhunter, I. (1886), Spherical Trigonometry: For the Utilise of Colleges and Schools, p. 129 ( Art. 163 )
28. ^ Lévy, Bruno; Liu, Yang (2010). " L _p Centroidal Voronoi Tessellation and its applications". ACM: 119.
29. ^ "Trouble 930" (PDF), Solutions, Crux Mathematicorum, 11 (5): 162–166, May 1985
30. ^ Wacław Sierpiński, Pythagorean Triangles, Dover Publications, 2003 (orig. ed. 1962), p. 107. Note however that Sierpiński repeats an erroneous adding of the volume of the Heronian tetrahedron example higher up.
31. ^ Federal Aviation Administration (2009), Pilot'southward Handbook of Aeronautical Cognition, U. S. Government Printing Office, p. 13-10, ISBN9780160876110 .
32. ^ Klein, Douglas J. (2002). "Resistance-Distance Sum Rules" (PDF). Croatica Chemica Acta. 75 (ii): 633–649. Archived from the original (PDF) on 10 June 2007. Retrieved 15 September 2006.
33. ^ Záležák, Tomáš (18 October 2007); "Resistance of a regular tetrahedron" ^{[ permanent dead link ]} (PDF), retrieved 25 Jan 2011
34. ^ Vondran, Gary L. (April 1998). "Radial and Pruned Tetrahedral Interpolation Techniques" (PDF). HP Technical Study. HPL-98-95: ane–32.
35. ^ Green, William Lowthian (1875). Vestiges of the Molten Globe, as exhibited in the effigy of the earth, volcanic activity and physiography. Vol. Part I. London: Eastward. Stanford. Bibcode:1875vmge.book.....G. OCLC 3571917.
36. ^ Holmes, Arthur (1965). Principles of concrete geology . Nelson. p. 32. ISBN9780177612992.
37. ^ Hitchcock, Charles Henry (Jan 1900). Winchell, Newton Horace (ed.). "William Lowthian Green and his Theory of the Evolution of the Earth's Features". The American Geologist. Vol. XXV. Geological Publishing Company. pp. 1–x.
38. ^ "Lightart-Biennale Austria 2010".
39. ^ "Marvin Minsky: Stanley Kubrick Scraps the Tetrahedron". Web of Stories. Retrieved twenty February 2012.
40. ^ Weisstein, Eric W. "Tetrahedral graph". MathWorld.

Bibliography [edit]

• Kepler, Johannes (1619). Harmonices Mundi (The Harmony of the World). Johann Planck.
• Coxeter, H.S.Chiliad. (1973). Regular Polytopes (3rd ed.). New York: Dover.

External links [edit]

• Weisstein, Eric W. "Tetrahedron". MathWorld.
• Gratuitous paper models of a tetrahedron and many other polyhedra
• An Amazing, Space Filling, Not-regular Tetrahedron that also includes a description of a "rotating ring of tetrahedra", also known as a kaleidocycle.

v t e Central convex regular and uniform polytopes in dimensions 2–10
Family	A north	B due north	I 2(p) / D n	Due east 6 / E vii / Due east viii / F 4 / G 2	Hn
Regular polygon	Triangle	Foursquare	p-gon	Hexagon	Pentagon
Uniform polyhedron	Tetrahedron	Octahedron • Cube	Demicube		Dodecahedron • Icosahedron
Compatible polychoron	Pentachoron	16-prison cell • Tesseract	Demitesseract	24-cell	120-cell • 600-cell
Uniform 5-polytope	5-simplex	v-orthoplex • 5-cube	5-demicube
Uniform 6-polytope	six-simplex	vi-orthoplex • 6-cube	half dozen-demicube	122 • ii21
Compatible 7-polytope	7-simplex	seven-orthoplex • vii-cube	7-demicube	132 • two31 • 321
Uniform 8-polytope	8-simplex	8-orthoplex • 8-cube	viii-demicube	ane42 • 241 • 421
Uniform 9-polytope	9-simplex	9-orthoplex • 9-cube	9-demicube
Compatible 10-polytope	ten-simplex	10-orthoplex • 10-cube	10-demicube
Compatible n-polytope	n-simplex	n-orthoplex • n-cube	n-demicube	onek2 • 2k1 • thou21	north-pentagonal polytope
Topics: Polytope families • Regular polytope • List of regular polytopes and compounds

holbrookpeatchath.blogspot.com

Source: https://en.wikipedia.org/wiki/Tetrahedron

Share this post